Fusionのスプライン表現

Fusionで自由曲線を作る場合、次の2つの曲線タイプがあります。

• フィット点スプライン(FiitedPointSpline）
• 制御点スプライン(ControlPointSpline)

この曲線の内部形式を見て、どのような形で保存されていて、何が違うのかをはっきりさせようというのが、この記事の内容です。答えはある程度分かっていて、保存形式はNurbsです。ただ、これは入れ物で合って、中身はベジエ曲線、B-Spline、 Nurbsが、Nurbs形式で管理されているのです。制御点スプラインは「ベジエ曲線」であることも分かっています。
フィット点スプラインがNurbsなのかB-Splineなのかがよくわからなかったのです。

まず、それぞれの曲線で第1象限に1/4円弧を書いてみます。
最初に制御点スプライン

図.制御点スプライン

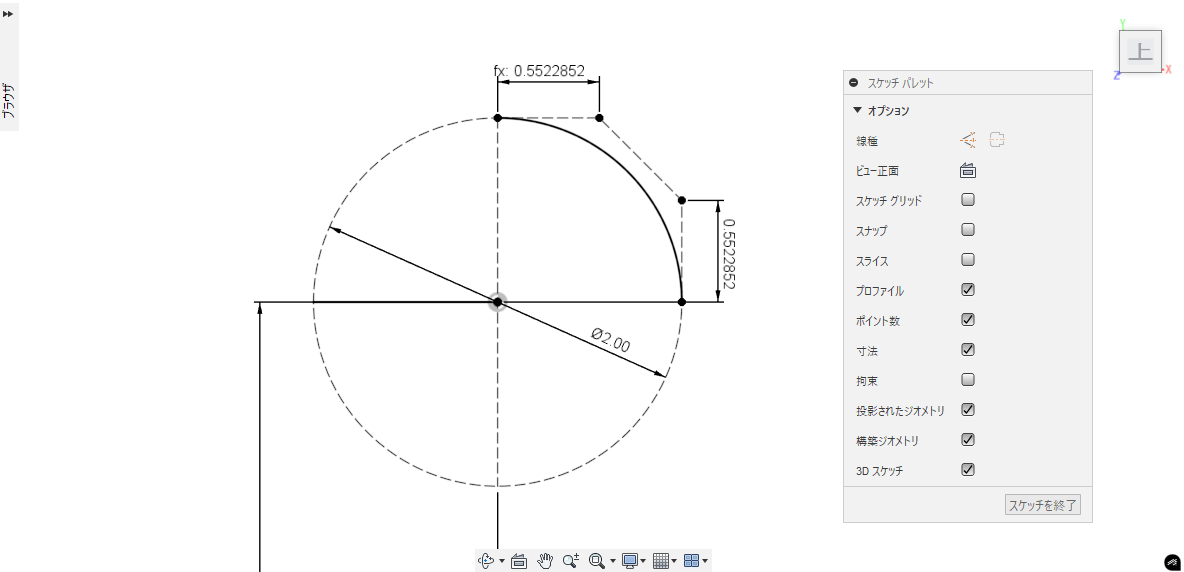
制御点スプラインというか、3次ベジエ曲線の円弧は、接線ハンドルの長さを半径×0.55228にとるとよいとされます。

• 制御点の距離 = 半径 × (4/3) × tan(π/8) ≈ 半径 × 0.55228

次にフィット点スプライン

図.フィット点スプライン

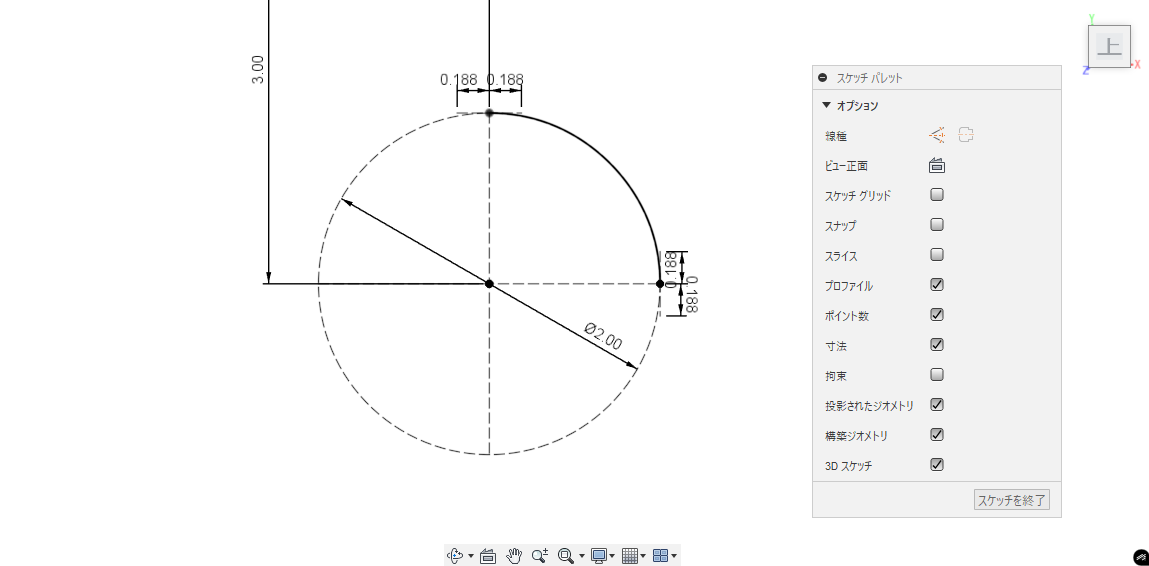
こちらは0.188にしていますが、目分量でなるべくぴったりになるよう合わせたものです。

Geom情報取得

この曲線の情報を得るには、曲線をピックしてから、次のコマンドを画面下段のテキストコマンド欄に入力します。

app = adsk.core.Application.get() ・・・・以降省略可能
app.executeTextCommand('sketch.GeomInfo' ) 

これで次の情報を得ました。
制御点スプライン

app.executeTextCommand(textCommand1) 
\t Geometry: id: 414 Spline3D Start point: (0, 0.1, 0) End point: (0.1, 0, 0)\nSpline details\n\tdegree: 3 \n\trational: 1 \n\tknots: 0 0 0 0 1 1 1 1 \n\tcontrol points: (0, 0.1, 0)(0.05522852, 0.1, 0)(0.1, 0.05522852, 0)(0.1, 0, 0) \n\tweights: 1 1 1 1

フィット点スプライン

app.executeTextCommand(textCommand1) 
\t Geometry: id: 467 Spline3D Start point: (0, 0.1, 0) End point: (0.1,0, 0)\nSpline details\n\tdegree: 5 \n\trational: 1 \n\tknots: 0 0 0 0 0 0 0.2 0.4 0.6 0.8 1 1 1 1 1 1 \n\tcontrol points: (0, 0.1, 0)(0.006971742880087394, 0.1, 0)(0.020378689477397946, 0.098938528152542754, 0)(0.038880625084621694, 0.09416466866241438, 0)(0.060504226681762162, 0.082226752495383262, 0)(0.082226752495380542, 0.060504226681764237, 0)(0.094164668662412312, 0.038880625084622381, 0)(0.09893852815254249, 0.020378689477398088, 0)(0.1, 0.0069717428800874209, 0))((-0.1,0, 0) \n\tweights: 1 1 1 1 1 1 1 1 1 1 

見にくいので整理すると

// 制御点スプライン（ID: 414）
const spline1 = {
id: 414,
type: "Spline3D",
startPoint: [0, 0.1, 0],
endPoint: [0.1,0, 0],
degree: 3,
rational: 1,
knots: [0, 0, 0, 0, 1, 1, 1, 1],
controlPoints: [
[0, 0.1, 0],
[0.055228512, 0.1, 0],
[0.1, 0.05522852, 0],
[0.1, 0, 0]
],
weights: [1, 1, 1, 1]
};

// フィットスプライン（ID: 467）
const spline2 = {
id: 467,
type: "Spline3D",
startPoint: [0, 0.1, 0],
endPoint: [0.1,0, 0],
degree: 5,
rational: 1,
knots: [0, 0, 0, 0, 0, 0, 0.2, 0.4, 0.6, 0.8, 1, 1, 1, 1, 1, 1],
controlPoints: [
[0, 0.1, 0],
[0.006971742880087394, 0.1, 0],
[0.020378689477397946, 0.098938528152542754, 0],
[0.038880625084621694, 0.09416466866241438, 0],
[0.060504226681762162, 0.082226752495383262, 0],
[0.082226752495380542, 0.060504226681764237, 0],
[0.094164668662412312, 0.038880625084622381, 0],
[0.09893852815254249, 0.020378689477398088, 0],
[0.1, 0.0069717428800874209, 0],
[0.1, 0, 0]
],
weights: [1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
};

Claudeで分析

これを、Claudeに分析してもらうと、フィット点スプラインは5次のBスプラインとなります。

3Dスプライン曲線データの整理
スプライン1（ID: 414）- 3次ベジェ曲線

次数: 3次
制御点数: 4点
開始点: (0, 0.1, 0)
終了点: (0.1, 0, 0)
形状: 右上から右下への滑らかな曲線（90度の円弧に近い）

スプライン2（ID: 467）- 5次B-スプライン

次数: 5次
制御点数: 10点
開始点: (0, 0.1, 0)
終了点: (-0.1, 0, 0)
形状: 右上から右下への滑らかな曲線（より複雑な形状）

判別方法

以下に判別方法を解説してもらいました。

Fusion 360では、すべての曲線が内部でNURBS形式で表現されていますが、データの特徴からベジエ曲線、Bスプライン、NURBSを区別できます。

各曲線タイプの特徴

ベジエ曲線（Bezier Curve）

• 制御点の数: 次数 + 1
• ノットベクトル: 特殊なパターン
• 3次ベジエ: [0,0,0,0, 1,1,1,1]
• 2次ベジエ: [0,0,0, 1,1,1]
• 特徴: 端点で制御点と一致、中間点は制御点の影響を受ける

Bスプライン（B-Spline）

• 制御点の数: 任意（次数 + 1以上）
• ノットベクトル: 一様または非一様
• 一様Bスプライン: [0,1,2,3,4,5,6,7]
• 非一様Bスプライン: 任意の値
• 特徴: 端点で制御点と一致しない場合がある

NURBS（Non-Uniform Rational B-Spline）

• 制御点の数: 任意
• ノットベクトル: 非一様
• 重み: 各制御点に重みが付く
• 特徴: 最も柔軟な表現

用語解説

ノットベクトル（Knot Vector）

定義

• ノットベクトルとは、NURBS曲線のパラメータ空間を定義する値の配列です。

役割

• パラメータ範囲の定義: 曲線のパラメータtの範囲を指定
• 基底関数の制御: Bスプライン基底関数の形状を決定
• 曲線の連続性: 曲線の滑らかさを制御

例

# 2次ベジエ曲線のノットベクトル
knots = [0, 0, 0, 1, 1, 1]
# 意味: パラメータtは0から1の範囲、端点で重複度3

規則

• 長さ: 制御点の数 + 次数 + 1
• 単調増加: 値は単調に増加する必要がある
• 重複度: 端点では次数+1回重複

有理（Rational）

定義

• 有理とは、制御点に重み（weight）が付いていることを意味します。

数学的表現

# 非有理（Non-rational）
P(t) = Σ Ni,p(t) * Pi

# 有理（Rational）
P(t) = Σ Ni,p(t) * wi * Pi / Σ Ni,p(t) * wi

特徴

• 非有理: 重みがすべて1.0、または重みなし
• 有理: 重みが1.0以外の値を持つ

用途: 円弧や円などの正確な表現が可能

• 例

# 非有理Bスプライン
weights = [1.0, 1.0, 1.0, 1.0]  # すべて1.0

# 有理NURBS
weights = [1.0, 2.0, 1.0]  # 異なる重み

重み（Weights）

定義

• 重みとは、各制御点の影響力を表す数値です。

効果

• 重み = 1.0: 標準的な影響力
• 重み > 1.0: 制御点の影響力が増加
• 重み < 1.0: 制御点の影響力が減少

視覚的効果

# 重みの効果
weights = [1.0, 2.0, 1.0]
# 中央の制御点の影響力が2倍になり、曲線がその点に引き寄せられる

特殊なケース

# すべての重みが1.0の場合
weights = [1.0, 1.0, 1.0, 1.0]
# 実質的に非有理Bスプラインと同じ

一様（Uniform）

定義

• 一様とは、ノットベクトルの値が等間隔であることを意味します。

一様Bスプライン

# 一様ノットベクトル
knots = [0, 1, 2, 3, 4, 5, 6, 7, 8]
# 特徴: 値が等間隔（1ずつ増加）

非一様Bスプライン

# 非一様ノットベクトル
knots = [0, 0, 0, 0, 1, 2, 3, 4, 5]
# 特徴: 値が不均等（開始部分で重複）

違いの効果

• 一様Bスプライン
  • 特徴: 滑らかで予測可能
  • 用途: 一般的な形状設計
  • 制御: 制御点の影響が均等
• 非一様Bスプライン
  • 特徴: 端点での制御が可能
  • 用途: 精密な形状制御
  • 制御: 端点での重複により端点通過性を制御

実用的な判別方法
1. ノットベクトルの判別

def isUniformKnots(knots):
    """一様ノットベクトルかチェック"""
    for i in range(1, len(knots)):
        if knots[i] - knots[i-1] != 1:
            return False
    return True

2. 有理性の判別

def isRational(weights):
    """有理曲線かチェック"""
    if not weights:
        return False
    for weight in weights:
        if abs(weight - 1.0) > 1e-10:
            return True
    return False

3. 重みの効果確認

def analyzeWeights(weights):
    """重みの分析"""
    if not weights:
        return "重みなし（非有理）"
    
    all_one = all(abs(w - 1.0) < 1e-10 for w in weights)
    if all_one:
        return "すべて1.0（実質的に非有理）"
    else:
        return f"有理（重み: {weights}）"

これらの概念を理解することで、NURBS曲線の特性を正確に把握し、適切な曲線タイプを選択できるようになるはず。