Fusion：数式カーブアドインでインボリュート歯形を作成する

Fusionのスケッチで、数式からスプラインカーブを生成するアドイン「CurveGenerator」を前回紹介しました。今回は、「CurveGenerator」をインボリュート歯車のモデリングに使った例を紹介します。

結果

ラックの歯先丸みを考慮する場合としない場合の2回に分けて説明します。

ラックの歯先丸み０の場合

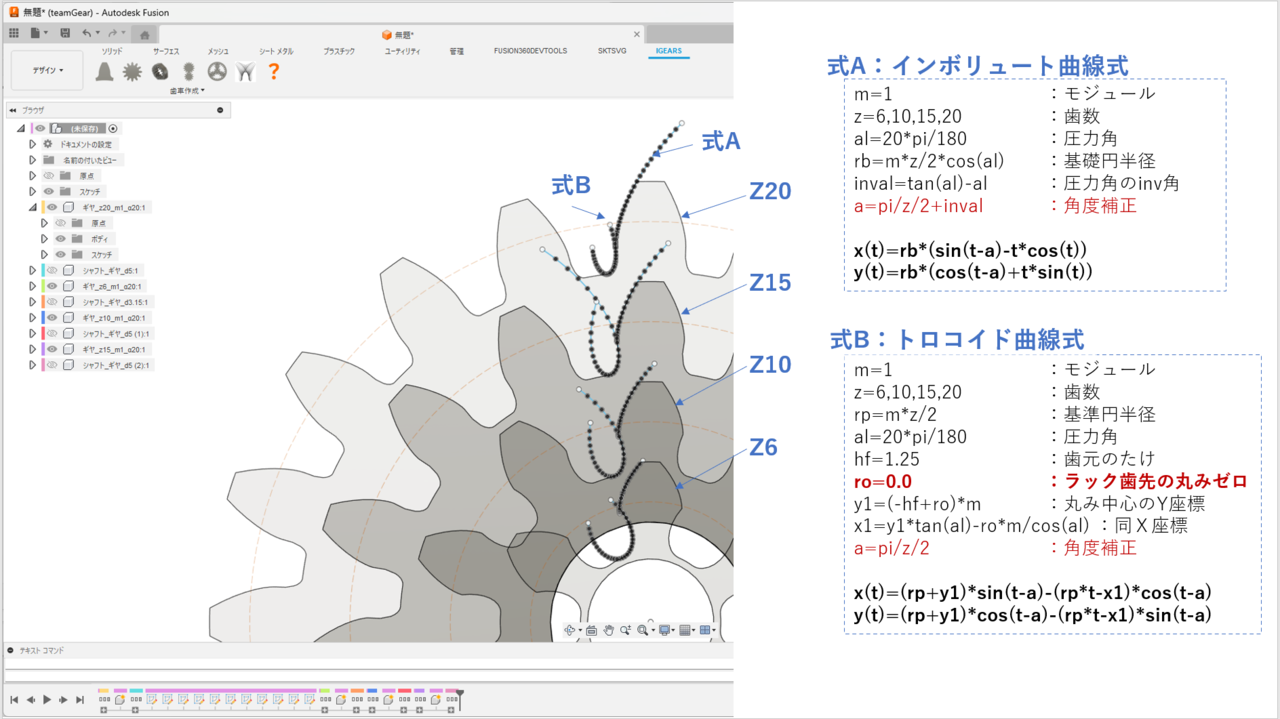
下図はギヤ作図アドイン「igears」で描いた歯数6,10,15,20のインボリュート歯車の正面図上に、「CurveGenerator」で作図した式A:インボリュート曲線、式B:トロコイド曲線を重ね書きしたものです。両者は完全に一致しています。

図1.結果

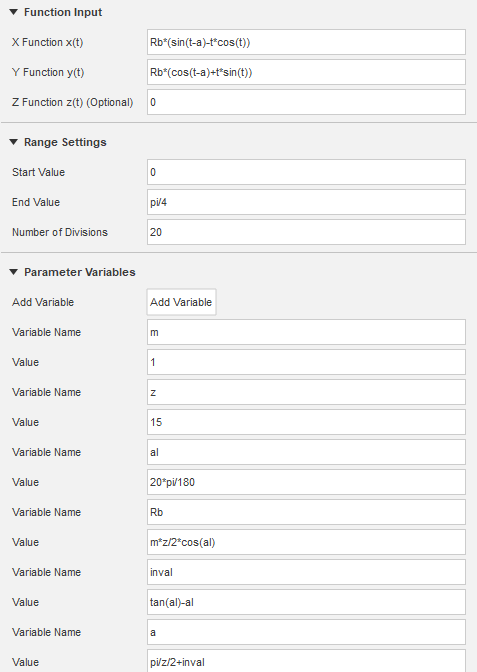
インボリュート計算式

• m=1 ：モジュール
• z=6,10,15,20 ：歯数
• al=20*pi/180 ：圧力角
• rb=m*z/2*cos(al) ：基礎円半径
• inval=tan(al)-al ：圧力角のinv角
• a=pi/z/2+inval ：角度補正
• x(t)=rb*(sin(t-a)-t*cos(t))
• y(t)=rb*(cos(t-a)+t*sin(t))

• • 角度補正：

歯形中心が角度t=0となるための補正量

「CurveGenerator」のダイアログに、次のように入力します。

図2.インボリュート曲線の入力

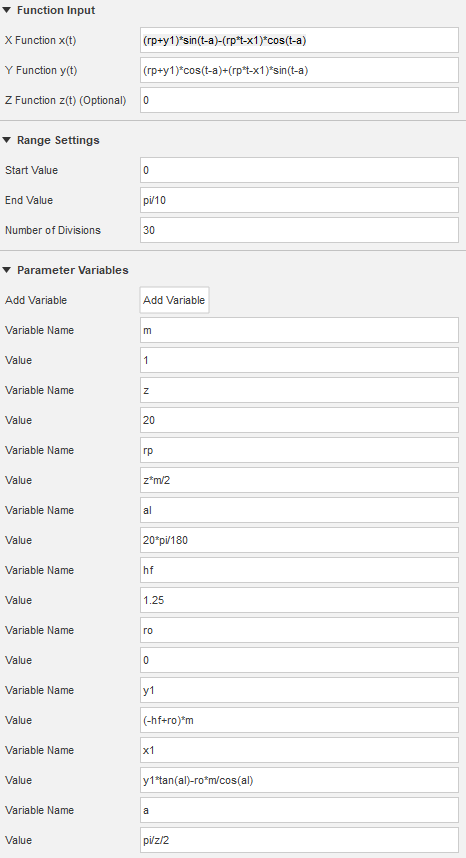
トロコイド計算式

• m=1 ：モジュール
• z=6,10,15,20 ：歯数
• rp=m*z/2 ：基準円半径
• al=20*pi/180 ：圧力角
• hf=1.25 ：歯元のたけ
• ro=0.0 ：ラック歯先の丸みゼロ
• y1=(-hf+ro)*m ：丸み中心のY座標
• x1=y1*tan(al)-ro*m/cos(al) ：同Ⅹ座標
• a=pi/z/2 ：角度補正
• x(t)=(rp+y1)*sin(t-a)-(rp*t-x1)*cos(t-a)
• y(t)=(rp+y1)*cos(t-a)-(rp*t-x1)*sin(t-a)

• • 角度補正：

歯形中心が角度t=0となるための補正量

「CurveGenerator」のダイアログに、次のように入力します。

図4.トロコイド曲線の入力

ラックの歯先丸みを考慮した場合は、別途アップします。