歯車がかみ合うということ

よく歯車の入門書に次のような記述があります。

2つの歯車がかみ合う条件は、同一モジュール、同一圧力角であること
歯車対がかみ合うためにはモジュールが等しくなければなりません

入門としてはそれでもいいのですが、実際には圧力角とモジュールが異なっていてもかみ合う場合があるのです。その条件とは

2つの歯車の法線ピッチが等しいこと

です。

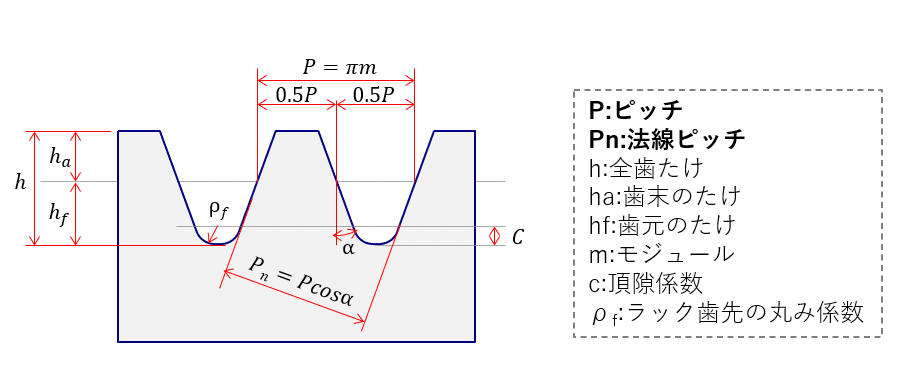
歯車のピッチ*1は、 $m$ ：モジュール、 $α$ ：圧力角として
$p=mπ$
です。法線ピッチ*2は
$p_n=p\cosα=mπ\cosα$
となります。2つの歯車で $p_{n1}$ と $p_{n2}$ が等しければいいので
$m_1\cos α_1=m_2\cos α_2$
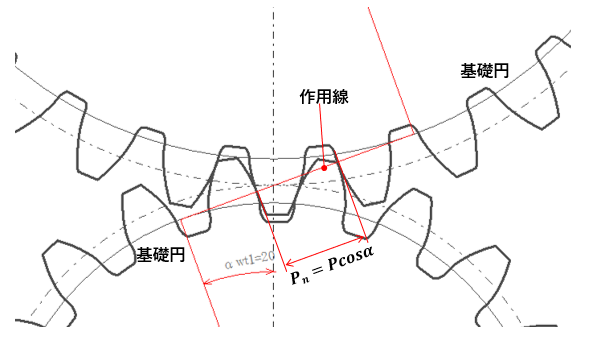
が成立していれば、圧力角とモジュールが違ってもかみ合うのです。両歯面のかみ合いの接触と進行は作用線*3に沿って行われますから、作用線上でピッチが同一であればかみ合うということです。

試してみましょう。
$m_1=2、α_1=20°、α_2=25°$ のとき、
$m_2=m_1\cos α_1/\cos α_2=2.0736$

Fusion360で3Dモデルを作ってモーションスタディしました。たしかに、歯面の隙間や干渉はなく、きれいにかみ合っているようです。

左側モデル
- 小歯車：歯数15、圧力角20°、モジュール2、法線ピッチ5.904
- 大歯車：歯数20、圧力角25°、モジュール2.0736、法線ピッチ5.904
右側モデル
- 小歯車：歯数15、圧力角25°、モジュール2.0736、法線ピッチ5.904
- 大歯車：歯数20、圧力角20°、モジュール2、法線ピッチ5.904

youtu.be