CADでラック歯形を作る(1)

前書き

歯車の加工法

歯車の形状は、JIS1702で規定される基準ラックを断面形状とするホブと歯車素材が同期回転することで切削加工されます。ラック（つまりホブ）は直線切れ刃ですが、加工後の歯車はインボリュート曲線です。工具に所定の運動を与えて、元の工具形状とは異なる曲線を加工する方法を「創成加工」といいます。これに対して完成品形状と同一形状の工具で切削加工する方法を「成型加工」といいます。

創成加工は切削に限らず研削でも使われます。スイスの「マーグ研削盤」が有名で旧JIS0級の高精度が得られるそうです。

ホブ加工とラック加工

以下の動画は筆者がFusion360で作成したもので、上がホブ加工、下がラック加工です。ホブはラックの平行移動運動を回転運動で実現するので、加工時間が短く、大量生産に向いています。動画のラック加工は、Fusion360のスクリプトでラックと歯車素材を作成し、所定の相対運動を与えながら、干渉部を除去することを繰り返しています。
www.youtube.com

歯元の形状の重要性

ところで、歯車のかみ合い部分はインボリュート曲線なのですが、歯底からインボリュート曲線までの曲線（歯元隅肉曲線）はなにか、疑問に思ったことはありませんか。

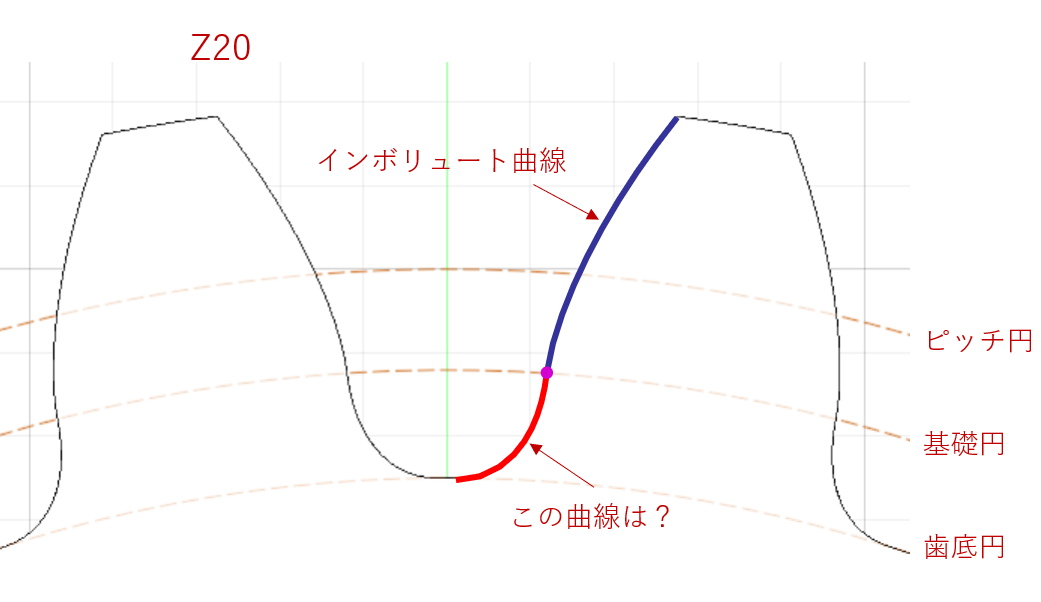
歯元隅肉曲線も、ホブ（ラック）の創成加工によって生じる形状で、「トロコイド曲線」（正確にはトロコイドの平行曲線）です。

歯に過大荷重が加わったときや疲労破壊するときには、隅肉部に亀裂を生じます。この亀裂位置を近似的に求める方法が「Hoferの30°接線法」で、「CADで危険断面と歯形係数を求める」で説明しています。
歯形係数が危険断面幅の二乗に反比例することと、危険断面位置での隅肉曲線の曲率半径が小さいほど応力集中係数が増大することから、隅肉曲線の形状が重要なのです。

歯元隅肉曲線の形状を決める因子は、加工方法、ラック形状、転位、歯数などです。ラックはインボリュート曲線を創成する部分と歯底にクリアランスを設けるための頂隙部分で構成されます。歯車素材の歯底にできるだけ大きい曲率半径の隅肉曲線を形成するためには、ラックの歯先を取りえる最大Rで丸める必要があります。このRのことを「ラック歯先の丸み」といいますが、通常はモジュールで除して「ラック歯先の丸み係数」で表します（=フィレット半径/モジュール）。

下図はJIS1701で定義される「基準ラック」の形状で、歯車の半径を無限大にしたときの歯形です。「基準ラック」をオス型とすれば、それを加工する「ラック」は歯と隙間部を反転したメス型なのでご注意ください。

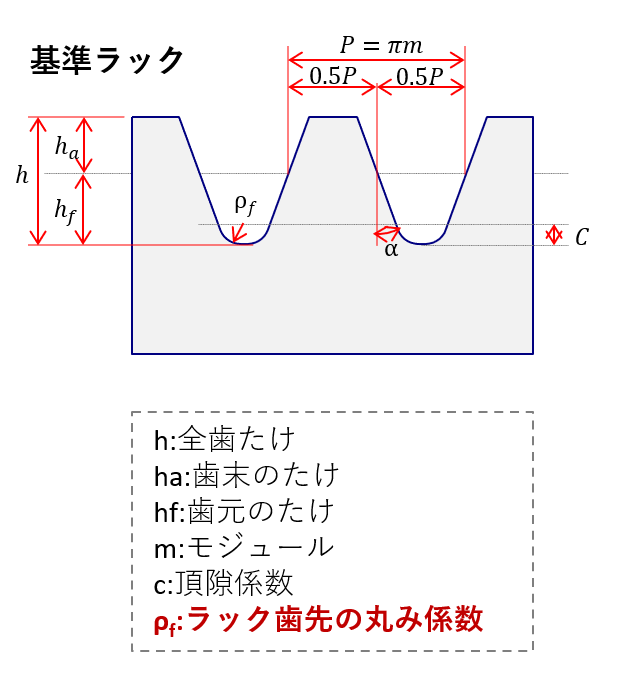
ラック歯先の丸み係数は、頂隙係数cとともに変化します。

頂隙係数c	歯先の丸み係数ρf
0.25	0.38(,資料によっては0.375)
0.40	0.39

この記事のねらい

前置きが長くなりましたが、この記事では上記の理解を深めるため、頂隙とラック歯先の丸み係数の関係をFusion360で求めてみます。

ラックが書けたら第2段階としてラックによる創成図、第3段階としてラックによる創成加工計算を考えています。スクリプトでは完成しているのですが、手作業でやる予定です。

ラックの作図(c0.25の場合)

ベース形状

モジュール $m1$ 、圧力角 $α20deg$ 、頂隙 $c0.25$ のラックを作成するとします。
ピッチ $p=m\cdot π$ なので歯幅は $p/2=1\cdot π/2=1.571$ です。
左右辺の傾きが20°対称でピッチ線位置での間隔が1.571、ピッチ線から上に1、下に1.25の台形のうち、左右辺と下辺を作図します。

歯先に丸みを付ける

ベースの形状の歯先部分に丸みを付けるのですが、条件として

丸みは始点終点が頂隙領域(c0.25)内で、歯形の中央を越えないこと
丸みは少なくとも一方の斜辺と下辺に接すること

とします。

丸み半径の幾何計算方法は後述しますが、ここではCADの作図で求めます。

まず、c0.25の領域内で「作成」「2接触指定の円」コマンドで斜辺と下辺に接する円と接触点への垂線を作図し、その交点をp,qとします。2接触円の半径は指定しません。

次に点pを、斜辺上の点sに「一致拘束」すると、2接触のままで最大Rの円に拡大または縮小されます。このときの2接触円の半径が「0.38」なのですが、詳しくみると「0.37995」を丸めていることが分かります。これをモジュールm1で割った数値が先ほどの表にある

頂隙係数c	歯先の丸み係数ρf
0.25	0.38、資料によって0.375

の0.38のことを指します。「資料によって0.375」というのは、おそらくですが、0.38だとわずかにインボリュート領域まで丸みがかかってしまうのを嫌って、0.005の余裕を見たのではないかと思います。0.379というのも見たことがあります。

今回はm1歯形だったので、丸み係数と実半径は等しい数値ですが、一般的に実半径は丸み半径係数にmを乗じて使ってください。

幾何計算で求める

先ほどの最大Rは、簡単な幾何計算で求められます。上図で $o'p'$ と $o'q'$ の長さは $R$ です。 $o'q'$ は $R\cos α$ と $c$ の和としても表せますから、次式が得られます。図示していませんが、 $α$ は圧力角なので、 $o'p'$ の傾きも $α$ になります。
$R=R \sin α+c$
整理移項して
$R(1-\sin α)=c$
∴
$R = \dfrac{c}{1-\sin α}=\dfrac{0.25}{1-\sin 20}=0.37995$
当然ですが、同じ値となります。この式は「JIS B 1701-1:2012 円筒歯車―インボリュート歯車歯形―第1部」に記載があります。

ラックの作図(c0.40の場合)

ベース形状

c0.25の場合とほぼ同じですが、頂隙部cだけ0.40に変更します。

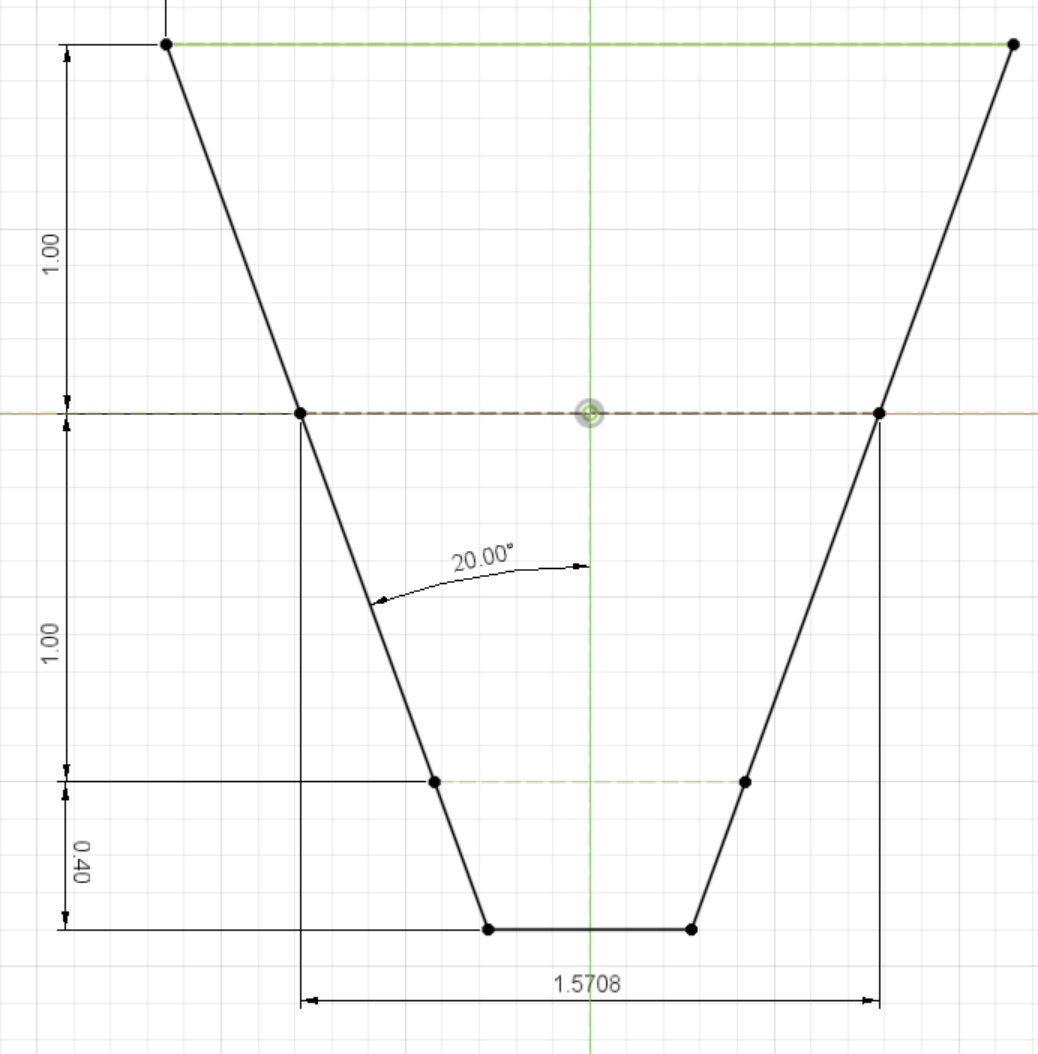
歯先に丸みを付ける

同様の方法でc0.4の領域内で「作成」「2接触指定の円」コマンドで斜辺と下辺に接する円と接触点への垂線を作図し、その交点をp,qとします。

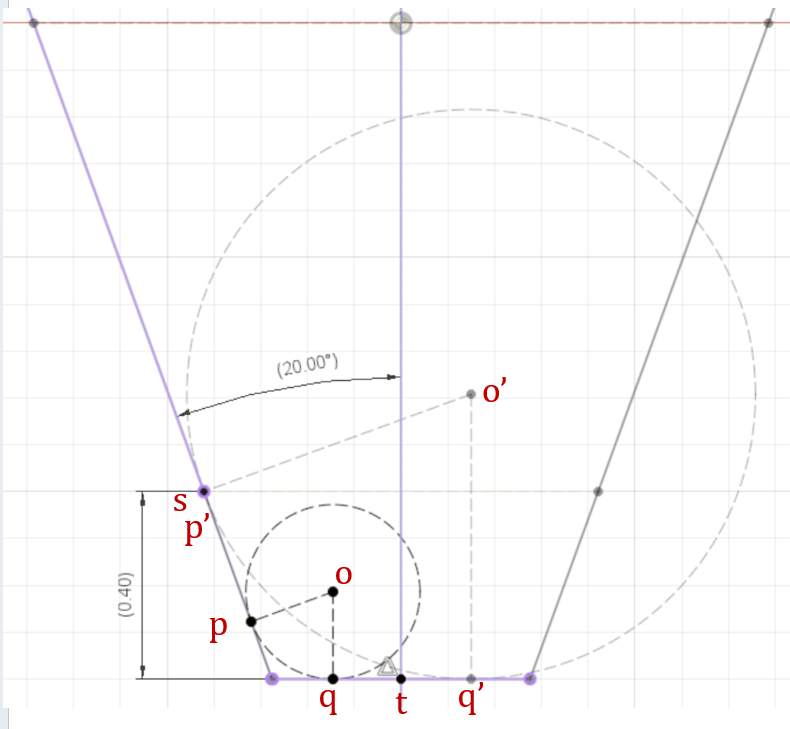
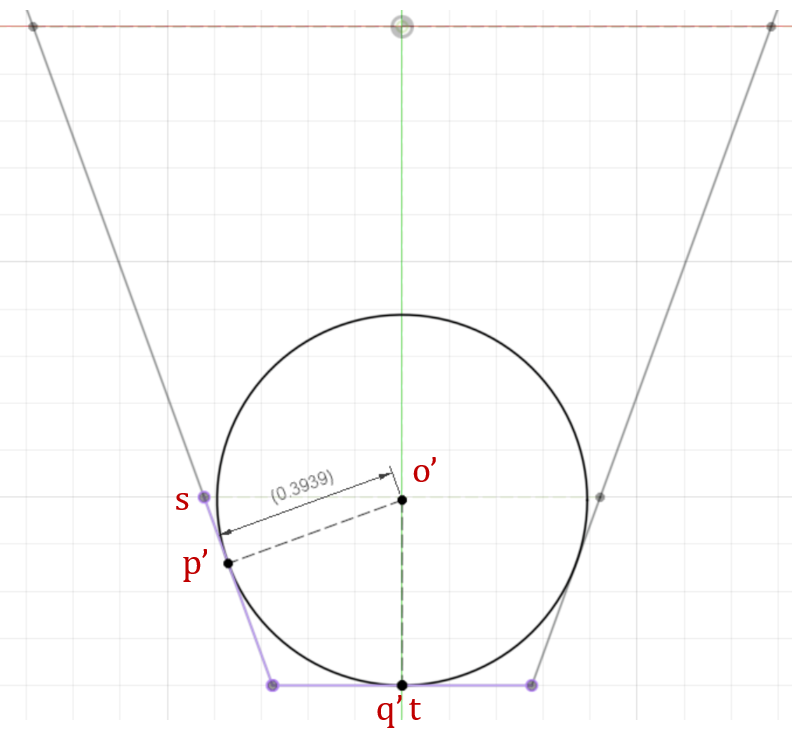
次も同様に点pを点sに一致拘束させると、点qが歯形の中央点tを越えてしまいます（上図参照）。
この場合は、点qを点tに一致拘束させたときが最大R0.3939となり、

次表の

頂隙係数c	歯先の丸み係数ρf
0.40	0.39

の0.39のことを指します。

幾何計算で求める

「JIS B 1701-1:2012 円筒歯車―インボリュート歯車歯形―第1部」に記載の次式に代入すると同じ値を得ます。
$R=\dfrac{\pi/4-(1+c)\tan α}{\tan ((90-α)/2)}=\dfrac{\pi/4-(1+0.4)\tan 20}{\tan ((90-20)/2)}=0.3939$
式の導出はしませんが、式中の $\pi/4$ はピッチ円位置での歯幅 $\pi/2$ の1/2ですから、幅方向の幾何関係からRを求めています。

まとめ

ラック歯先の丸みは、簡単な制約条件を満足する最大半径を取っているだけで、頂隙係数の関数になります。丸み中心が歯形の中心にあるときはフルRとなります。なお、最大半径に限定するわけではなく、それ以下であってもかまいません。

頂隙係数cは、加工方法で決まります。ホブ切りだけの場合は0.25ですが、後工程でシェービングや歯研を行う場合は、工具と歯底の干渉を避けるために0.35～0.4とします。ホブ後シェービングのように複数の歯面加工を行う場合は、隅肉に段差を生じることがあり、これを回避するために「プロチューバランス（こぶ付き）ホブ」を使う場合があります。

Fusion360用の無料歯車作成アドインのうち、頂隙係数を指定できるのはHelical Gear Plus とigears2ですが、Helical Gear Plusはそもそも簡易歯形なので正確な歯元形状は分かりません。Helical Gear Plusが頂隙係数指定可能なことによるメリットは、正しい歯底円径が得られることです。
さらに丸み係数まで指定できるのはigears2です。歯車専門家向けのソフトだと、頂隙係数と丸み係数両方を指定できるのが普通です。

まとめになっていませんが、とりあえず1回目はこれで終わります。